1.K-Means定义:
K-Means是一种无监督的基于距离的聚类算法,简单来说,就是将无标签的样本划分为k个簇(or类)。它以样本间的距离作为相似性的度量指标,常用的距离有曼哈顿距离、欧几里得距离和闵可夫斯基距离。两个样本点的距离越近,其相似度就越高;距离越远,相似度越低。
目的是,实现簇内的距离尽量小(紧凑),而簇间的距离尽可能大(分开)。 我们使用误差平方和SSE作为聚类质量的目标函数,该值越小表明样本簇内较紧密。
1.1关键问题:
- (1)k值的选择(法一:根据经验;法二:借助交叉验证选。评价k值的好坏,有手肘法(以簇内误差平方和SSE作为度量聚类质量的目标函数,以误差平方和较小的作为最终聚类结果,通过作图,快速辨认变化较大对应的k值,参考刘顺祥kmeans实操内容)、轮廓系数Silhouette Coefficient(from sklearn.metrics import silhouette_score 可计算,结果在[-1,1]之间,越大代表内聚度和分离度相对较好)和Calinski-Harabasz Index(在sklearn中,有metrics.calinski_harabaz_score,分数越高越好)。
- (2)k个质心的选择方式 (质心之间最好不要太近)
1.2例子讲解:
借助下图,讲解最简单的2个分类问题:
(a)给出的样本数据
(b)随机选取2个样本点作为质心,一个红色a1,一个蓝色b1(选取的样本可以不在原始样本中) (c)计算所有样本到这两个质心的距离,and then 将样本划分到两个距离中距离较小的那一类中。于是,样本分成了红蓝两派。 (d)对c图中的红蓝两派,找出对应簇的新的质心:a2、b2,并标记其位置。 (e)重新计算所有样本到质心:a2、b2的距离,and then 将样本划分到两个距离中距离较小的那一类中。于是,样本被重新划分成了两类。 (f)重复d、e步,直到质心的位置不再变化。2.python操作:
在sklearn中,一般用sklearn.cluster.KMeans解决问题。
针对数据量非常大的情况,如样本量>10万,特征数量>100。这时就要用Mini Batch K-Means解决问题。它抽取原始样本中的部分样本作为新的样本集来聚类,这样会降低聚类的精确度(这一般在可接受范围内),但是减少了计算的时间。python官方文档:
- sklearn.cluster.KMeans:
- sklearn.cluster.MiniBatchKMeans:
2.1 KMeans类
sklearn中的KMeans算法仅支持欧式距离,因为其他距离不能保证算法的收敛性。
class sklearn.cluster.KMeans(n_clusters=8, init=’k-means++’, n_init=10, max_iter=300, tol=0.0001, precompute_distances=’auto’, verbose=0, random_state=None, copy_x=True, n_jobs=None, algorithm=’auto’)
- (1)n_clusters :聚类个数k,默认为8.
- (2)init :{‘k-means++’, ‘random’ or an ndarray} ,质心的选择方式, 默认为‘k-means++’. ‘random’:随机选取k个质心. ‘k-means++’ :普通版KMeans的优化版,随机选取一个质心后,计算所有样本到质心1的距离,然后根据距离选取新的质心2,接着计算样本到最近质心的距离,再选出质心3,重复计算距离,直至找到k个质心为止。是对随机选取的一个优化版。
- (3)n_init :int,默认为10. 设置重复该算法次数m,每次选取不一样的质心,然后选取这m个结果的最优output。
- (4)max_iter :int, default: 300 单次运行的k-means算法的最大迭代次数
- (5)random_state :设置数据复现的参数
- (6)algorithm :有三种参数设置,“auto”, “full” or “elkan”,默认是”auto”. 最基础的KMeans用“full”,而“elkan”利用三角不等式(两边之和大于第三边、两边之差小于第三边)减少距离的计算,加快算法的迭代速度,是对基本版KMeans的优化,但它不适用于稀疏数据. 对于稠密数据,“auto” 会选用“elkan” ,对于稀疏数据,会用 “full”.
对应Attributes:
- (1)cluster_centers_ : 输出聚类的质心
- (2)labels_ :输出样本聚类后所属的类别
- (3)inertia_ : 浮点型,输出簇内离差平方和
- (4)n_iter_ : 整数,输出运行的迭代次数
先用make_blobs产生聚类数据,再用KMeans进行分类
from sklearn.datasets import make_blobs #产生聚类数据#5000个样本,每个样本有两个特征,质心为centers所给出,此例中有4个质心,每个类的方差由cluster_std给出,random_state为数据复现用x, y = make_blobs(n_samples=3000, n_features=2, centers=[[-1,-1], [0,0], [1,1], [2,2]], cluster_std=[0.4, 0.7, 0.2, 0.2], random_state =2019) #作图看原始数据import matplotlib.pyplot as plt%matplotlib inlineplt.scatter(x[:, 0],x[:,1])


令k=2、3、4,然后评估每个k值的好坏
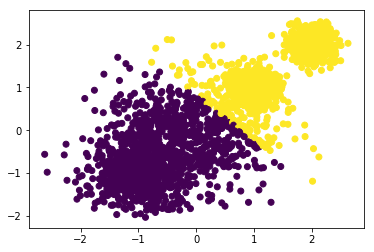
from sklearn.cluster import KMeansy_1 = KMeans(n_clusters=2, random_state=2020).fit_predict(x)plt.scatter(x[:, 0], x[:, 1],c=y_1)from sklearn import metricsmetrics.calinski_harabaz_score(x,y_1)
8255.3432347343351


y_2 = KMeans(n_clusters=3, random_state=2020).fit_predict(x)plt.scatter(x[:, 0], x[:, 1],c=y_2)metrics.calinski_harabaz_score(x,y_2)
9071.2281163994103

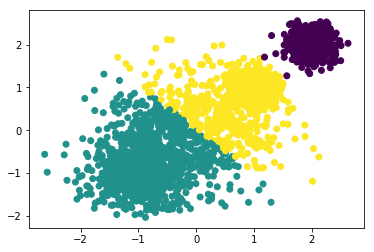
y_3 = KMeans(n_clusters=4, random_state=2020).fit_predict(x)plt.scatter(x[:, 0], x[:, 1],c=y_3)metrics.calinski_harabaz_score(x,y_3)
9151.6774896842526

随着k的递增,Calinski-Harabaz Index的分数也越来越高。分类成4个簇的分类效果最好。
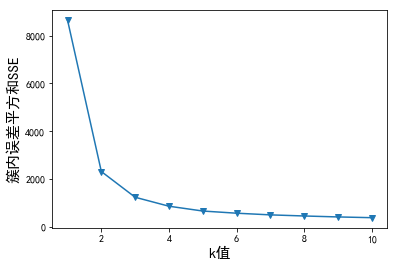
也可以利用簇内误差平方和来选择最佳K值:
SSE = []for i in range(1,11): #k取1-10,计算簇内误差平方和 km = KMeans(n_clusters=i, random_state=2019) km.fit(x) SSE.append(km.inertia_)plt.plot(range(1,11), SSE, marker='v') plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签plt.rcParams['axes.unicode_minus']=False #用来正常显示负号plt.xlabel('k值', size=15)plt.ylabel('簇内误差平方和SSE', size=15) 
2.2 MiniBatchKMeans类
class sklearn.cluster.MiniBatchKMeans(n_clusters=8, init=’k-means++’, max_iter=100, batch_size=100, verbose=0, compute_labels=True, random_state=None, tol=0.0, max_no_improvement=10, init_size=None, n_init=3, reassignment_ratio=0.01)
- (1)n_init:用不同的初始化质心运行算法的次数。每次用不一样的采样数据集来跑不同的初始化质心运行算法,与KMeans类有所区别。
- (2)batch_size:指定采集样本的大小,默认是100.如果数据集的类别较多或者噪音点较多,需要增加这个值以达到较好的聚类效果。
- (3)init_size: 用来做质心初始值候选的样本个数,默认是batch_size的3倍,一般用默认值就可以了。
- (4)reassignment_ratio: 某个类别质心被重新赋值的最大次数比例,这个和max_iter一样是为了控制算法运行时间的。这个比例是占样本总数的比例,乘以样本总数就得到了每个类别质心可以重新赋值的次数。如果取值较高的话算法收敛时间可能会增加,尤其是那些暂时拥有样本数较少的质心。默认是0.01。如果数据量不是超大的话,比如1w以下,建议使用默认值。如果数据量超过1w,类别又比较多,可能需要适当减少这个比例值。具体要根据训练集来决定。
- (5)max_no_improvement:即连续多少个Mini Batch没有改善聚类效果的话,就停止算法, 和reassignment_ratio, max_iter一样是为了控制算法运行时间的。默认是10。
from sklearn.cluster import MiniBatchKMeansy_m1 = MiniBatchKMeans(n_clusters=2, batch_size=300, random_state=2019).fit_predict(x)plt.scatter(x[:,0], x[:,1], c=y_m1)print("当k=2时:",metrics.calinski_harabaz_score(x,y_m1)) 当k=2时: 8254.39452154

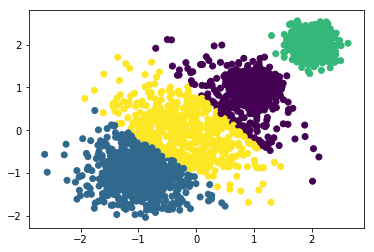
y_m2 = MiniBatchKMeans(n_clusters=3, batch_size=300, random_state=2019).fit_predict(x)plt.scatter(x[:,0], x[:,1], c=y_m2)print("当k=3时:",metrics.calinski_harabaz_score(x,y_m2)) 当k=3时: 9070.83967062


y_m3 = MiniBatchKMeans(n_clusters=4, batch_size=300, random_state=2019).fit_predict(x)plt.scatter(x[:,0], x[:,1], c=y_m3)print("当k=4时:",metrics.calinski_harabaz_score(x,y_m3)) 当k=4时: 9122.03629824

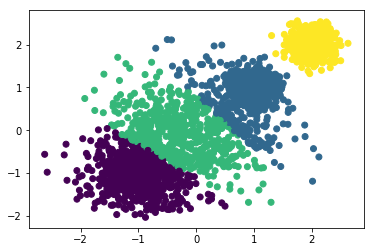
y_m4 = MiniBatchKMeans(n_clusters=5, batch_size=300, random_state=2019).fit_predict(x)plt.scatter(x[:,0], x[:,1], c=y_m4)print("当k=5时:",metrics.calinski_harabaz_score(x,y_m4)) 当k=5时: 9091.0670116

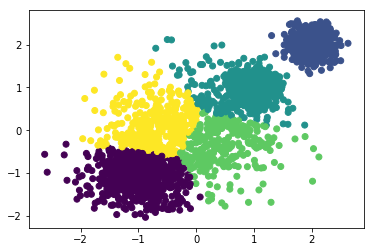
可以看到当抽取300个样本数据出来做KMeans时,k从1—>4增大时,calinski_harabaz_score逐渐递增。当k=4时,聚类效果最好,calinski_harabaz_score为9122。当k增大为5时,看到评分的下降,说明聚类为4类时最好。
抽样与不抽样的比较:用原始的3000个样本数据时,当k=4时,calinski_harabaz_score为9151,大于抽样时划分4类时对应的评分:9122。可见在用小样本时,精确度有所下降,但是最后聚类效果还是可以的。3.KMeans的优缺点:
1.算法原理比较简单,可解释性强,对凸数据的收敛较快。
2.较适用于样本集为团簇密集状的,而对条状、环状等非团簇状的样本,聚类效果较一般。 3.对事先给定的k值、初始质心的选择比较敏感,不同的选择可能导致结果差异较大。 4.最后的结果为局部最优,而不是全局最优。 5.对噪点、异常点较敏感。在实际操作中,注意:
(1)模型的输入数据必须为数值型数据,如果是离散型,一定要做哑变量处理。 (2)此算法是基于距离运算的,为防止量纲带来的影响,需要将数据标准化处理(零-均值规范) (3)最终聚类分析算法的评价,可用RI评价法(兰德指数)、F评价法、误差平方和、轮廓系数(Silhouette)、calinski-harabaz Index等,参考https://www.cnblogs.com/niniya/p/8784947.html。